Let’s talk about the energy. There is energy in things that move – and wind is no different.
Wind in motion contains energy that we can convert into electrical energy via turbines.
Let’s look at how much energy is in wind, and how turbines can capture it.
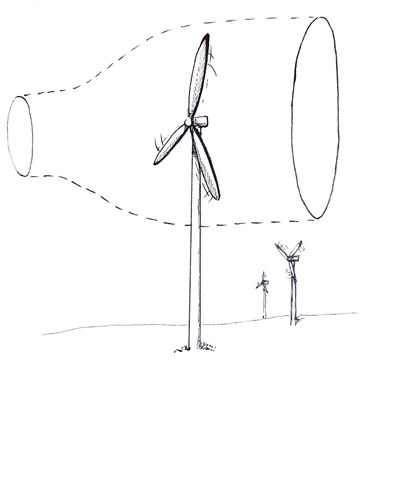
The wind cone as wind passes through the turbine
When the wind passes through the rotor swept area, some of the energy is transferred into the turbine, making it spin. When the energy is transferred, the wind loses speed. The same amount of wind travelling at a slower speed must take up more space – so the cone downstream[1] of a turbine is wider than before the turbine. This is what happens in the diagram above.
Energy Produced by A Turbine
So now we’ve established that wind transfers power to a turbine and loses speed while doing it. Let’s look at the math behind it[2].
Power Output of a Turbine = ½ * Air Density * Wind Speed3 * Rotor Swept Area * Power Coefficient
Let’s look at the different components:
- The air density varies slightly with temperature and altitude, but it’s around 1.225 kg/m3
- The wind speed is how fast the wind moves. Note that since this is cubed, aka multiplied with itself three times, a small difference in wind speed can make a huge difference in the power output.
- The Rotor Swept Area is how large an area the turbine blade sweeps. The larger the turbine blades, the bigger the Rotor Swept Area, and the more power can be captured.
- The Power Coefficient is an indicator about how effective the turbine is at extracting power from the wind. It varies with both blade pitch angle and the tip speed ratio, both which are explained below.
Optimizing Power Output of a Single Turbine
We’ve seen the equation that governs the amount of energy we can extract from wind. Let’s try to dive into what matters when we want to optimize this, so we can generate as much power as possible. This is a simple model, but hopefully it will give us some good intuition about what matters.
Wind Speed
This is the big one. As the wind speed is cubed in the equation above, small increases in wind speed means huge increases in power output. This means that a turbine operating at a wind speed of 10 m/s in will generate 8 times as much power as an identical turbine operating at 5 m/s.
That's why location is a huge deal when it comes to placing turbines and parks[3]. Placing parks in areas with slightly more wind, can result in a vastly larger power output.
Rotor Swept Area
All other things being equal, a bigger rotor swept area is better.
However, we can’t simply increase the rotor swept area without also making other things larger. For one, the tower must be tall enough that the blades don’t come too close to the ground.
But we also need to talk about weight here. If we make the rotor disc bigger, we need to make the entire turbine bigger so it can carry it. Due to the square cube law, when things increase in surface area, their volume also increases – just at a faster rate. In practice this means that if we double a wind turbine in size, the energy production will be four time as large due to the larger rotor area, but it will weigh eight times more[4]! This obviously leads to a much more expensive construction.
Power Coefficient
The power coefficient is a measure of how much energy the turbine manages to extract out of the wind.
The power coefficient has a theoretical maximum, called the Betz Limit, or Betz’s Law. The Betz Limit is 16/27 or 0.593. This means that the perfect turbine can at best capture 59.3% of the energy of wind that passes through it. Modern turbines operating at peak production can achieve power coefficients of 0.45-0.47, or 75-80% of the Betz limit.
The power coefficient is often given as a lookup table based on two things:
The Tip Speed Ratio
The tip speed ratio is a measure of how fast the tips of the turbines move in relation to the air around it.
If the blades move too slowly, most of the wind will simply pass through the turbine without giving off any energy.
If the blades move too quickly, they will seem like a solid wall to the wind, obstructing the wind flow and reducing power extraction.
The tip speed ratio is calculated by dividing the speed of the tips of the turbine with the wind speed. An optimal tip speed ratio depends on many things, but for 3-blade turbines it’s somewhere between 5-9 depending on the turbine design.
That means for a turbine with an optimal tip speed ratio of 9, where the wind blows at 10 m/s, the tips of the turbines must move at a staggering 90 m/s to achieve optimal tip speed ratio. This means that the blade tips of turbines that look like they’re revolving slowly, can be travelling at a fourth of the speed of sound or more.
The Blade Pitch Angle
The blades of the turbine can be pitched, meaning angled, to capture more or less energy. The turbines will pitch the blades differently depending on the wind speeds. We’ll cover this more in-depth in another post.
Other Factors
Note that these things are only true for a single turbine. There are other effects at play in Wind Parks, where the wake (downstream wind) of one turbine can influence the other turbines in the park.
The model above is also simplified. It doesn’t consider turbine yaw, meaning the direction of the turbine itself, turbulence and how multiple turbines interact with each other in a wind park. But it gives us a good intuition about what matters when talking turbine speed – and that’s good enough for now.
Written by Gustav Wengel, Software Engineer at SCADA MINDS.
Read more on Gustav's code adventures here.
[1] Downstream is "after" the turbine, Upstream is "before"
[2] Or rather, some of the math. Wind turbines and wind is extremely complex and can be modelled in many ways. This model is called the Actuator Disc Model, and it's pretty simple, but it works well for many cases, but there's also many factors it doesn't take into account, such as turbine yaw.
[3] Other factors such as tower height also factors in. Wind blows slightly more at higher altitudes. Particularly for onshore turbines, getting a bit away from the ground matters, because there can be turbulence because of the terrain.
[4] However, you can use different materials in the larger size, but the principles hold. Source in Danish: link

